Leetcode

2438. 二的幂数组中查询范围内的乘积/第 89 场双周赛 Q2/Rating 1610

• 位运算
• 前缀和
• 快速幂

考虑到 $2^a \times 2^b = 2^{a + b}$，所以可以对指数做前缀和，然后快速幂求解。

也可以不做前缀和，每次进行求和，然后快速幂求解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

MOD = 10 ** 9 + 7

def qp(x: int, k: int) -> int:
    ans = 1
    while k:
        if k & 1:
            ans = (ans * x) % MOD
        x = (x * x) % MOD
        k >>= 1
    return ans % MOD

class Solution:
    def productQueries(self, n: int, queries: List[List[int]]) -> List[int]:
        p = []
        for i in range(30):
            if n & (1 << i):
                p.append(i)
        ans = []
        for l, r in queries:
            ans.append(qp(2, sum(p[l:r+1])))
        return ans

Leetcode

869. 重新排序得到 2 的幂/第 93 场周赛 Q2/Rating 1505

• 排序
• 哈希

考虑到 $1 \leq n \leq 10^9$，可以直接枚举这个范围内的所有 $2$ 的幂进行哈希，只需要判断给定数字的哈希是否存在即可。

1
2
3
4
5
6

p = [sorted(str(1 << i)) for i in range(0, 31)]

class Solution:
    def reorderedPowerOf2(self, n: int) -> bool:
        s = sorted(str(n))
        return s in p

Codeforces

easy

CF2123E/Rating 1400

• 思维
• 差分
• 前缀和
• 正难则反

直接计算原问题是困难的，但是对于已经出现过的数，维护如何让序列的 $\mathrm{mex} = i$ 是容易的：

Leetcode

231. 2 的幂

• 位运算

太简单（

判一下二进制位上是否至多存在一个 1 即可。注意数据里面有负数（

1
2
3

class Solution:
    def isPowerOfTwo(self, n: int) -> bool:
        return n > 0 and n.bit_count() <= 1

Codeforces

easy

CF2057C/Rating 1500

• 位运算
• 贪心
• 构造

Leetcode

808. 分汤/第 78 场周赛 Q3/Rating 2397

• 概率 dp
• 诈骗

考虑朴素概率 dp：$dp_{i, j}$ 表示汤 $A$ 剩余 $i$ ml 且汤 $B$ 剩余 $j$ ml 时的答案。

显然有状态转移：

$$dp_{i, j} = \frac 14\left(dp_{i - 100, j} + dp_{i - 75, j - 25} + dp_{i - 50, j - 50} + dp_{i - 25, j - 75}\right)$$

边界情况：

• $i = j = 0$：此时两种汤只能被同时耗尽，根据题意有 $dp_{0, 0} = 0.5$；
• $i = 0, j > 0$：此时只能一直选择第一种操作，根据题意有 $dp_{0, j} = 1$；
• $i > 0, j = 0$：此时没有可选择的操作，根据题意有 $dp_{i, 0} = 0$。

1
2
3
4
5
6
7
8
9
10
11
12

class Solution:
    def soupServings(self, n: int) -> float:
        @cache
        def dfs(i: int, j: int) -> float:
            if i <= 0 and j <= 0:
                return 0.5
            if i <= 0:
                return 1.0
            if j <= 0:
                return 0.0
            return (dfs(i - 100, j) + dfs(i - 75, j - 25) + dfs(i - 50, j - 50) + dfs(i - 25, j - 75)) / 4
        return dfs(n, n)

此时并没有考虑 $n \leq 10^9$ 的数据范围，朴素的状态转移显然会超时。

语法分析

通过 ANTLR4 生成语法分析器

此处我们研究一个名为 Cymbol 的语言，是 C 语言的子集（代码附后）：

这样的文法有几个问题：

• 二义性：一段程序可以有多种解释方法。

  1 2 3 4

  stat: 'if' expr 'then' stat | 'if' expr 'then' stat 'else' stat | expr ;

  假设此时有这样的程序：if a then if b then c else d，会出现二义性：

  • if a then if b then c else d；
  • if a then if b then c else d。

  这种语法歧义被称为“悬空的 else”。

  如何修改这样有二义性的文法？

  我们将文法修改为：

  1 2 3 4 5 6 7 8 9

  stat: matched_stat | open stat ; matched_stat: 'if' expr 'then' matched_stat 'else' matched_stat | expr ; open_stat: 'if' expr 'then' stat | 'if' expr 'then' matched_stat 'else' open_stat ;

  改造后的文法实现了第一种解释。

  为什么？

  • 证明改造前后接受的语句集合是相同的；
  • 证明改造后的文法无二义性。

  证明留做习题（

  但是注意到，通过 ANTLR4 测试改造前的文法，发现同样实现的是第一种解释，并无二义性。原因是 ANTLR4 会按照从上向下的顺序分配优先级，越往上的优先级越高，所以这种实现也是正确的。

• 运算符的结合性带来的二义性：

  1 2 3 4

  expr: expr '*' expr | expr '-' expr | DIGIT ;

  对于此文法，1-2-3 会被解释为 (1-2)-3 或 1-(2-3)：

  

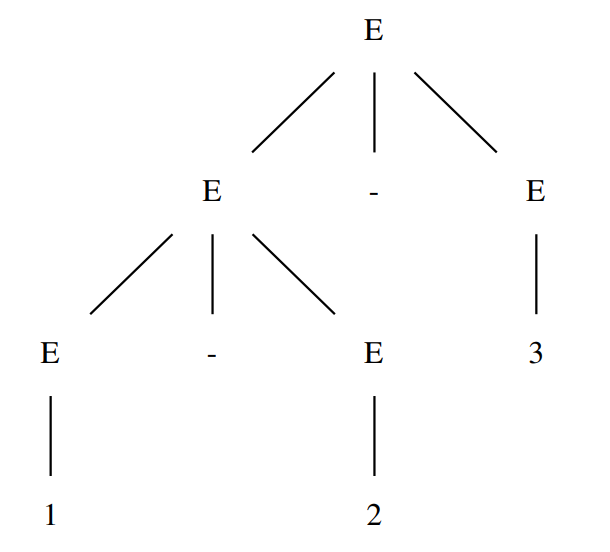
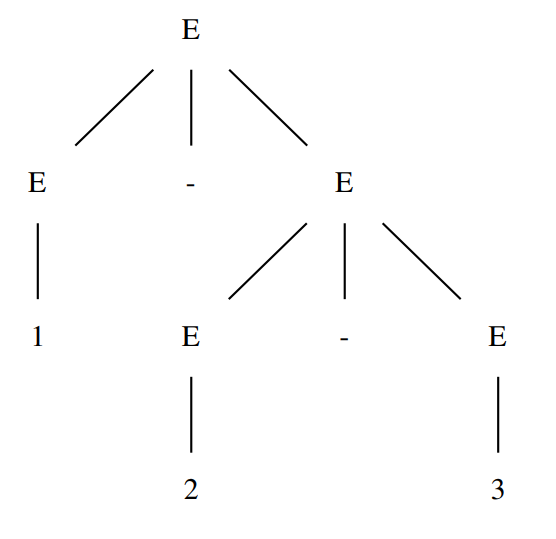
  在 ANTLR4 中，如果未明确运算符是左结合还是右结合，默认左结合，即上述表达式被解释为 (1-2)-3。

  如果想指定右结合，可以在语句前加入 <assoc = right>，如：

  1 2 3 4

  expr: '!' expr | <assoc = right> expr '^' expr | DIGIT ;

  考虑前缀运算符，这东西不带来歧义，只有一种解析方式，即右结合；后缀运算符只能左结合。

• 运算符的优先级带来的二义性：

  1 2 3 4

  expr: expr '*' expr | expr '-' expr | DIGIT ;

  当一个运算符优先级更高时，在解析树中的深度会更深。在 ANTLR4 中这样写已经可以处理优先级的问题，因为写在前面的优先级更高。

  如果不得已非要处理这种情况，可以通过两种方法：

  • 改为左递归（左结合）：

    1 2 3 4 5 6 7 8 9

    expr: expr '-' term | term ; term: term '*' factor | factor ; factor: DIGIT;

    如此，对于一个语法单元 expr，只会被左侧的 expr 调用递归，这被称为左递归文法，这样限制了文法只能被左结合的方式进行解释。

    由于乘号优先级更高，所以要把乘号放在右侧，等待 expr 被解释完成后再进行解释。

    左递归文法：e -> e - t -> e - t - t -> ...

  • 改为右递归：

    1 2 3 4 5 6 7

    expr: term expr_prime; expr_prime: '-' term expr_prime; term: factor term_prime; term_prime: '*' factor term_prime; factor: DIGIT;

    expr 表示的内容依然为 term-term-term-...，不同的是，通过引入新的语法单元 prime，expr 生成的方式为先生成一个 term，再不断生成 -term 序列，这样就是右递归文法了。

    右递归文法：e -> tEP -> t - tEP -> t - t - tEP -> ...

生成函数调用图

函数调用图表示的是函数之间的调用关系。

获取函数名有两个时机：

• 在进入 functionDecl 时，可以获得当前进入的函数名；
• 在遇到 functionCall 时，即找到一个 expr 表示的是 ID '(' exprList? ')' 时，我们就可以得到被调用函数的函数名（即 ID）。

只要在图中将这两个函数名连边即可。

词法分析

我们令 id 表示以字母开头的包含字母、数字的字符串，id 定义了一个集合，称之为语言（Language）。

id 中使用了字母、数字等符号集合，称之为字母表（Alphabet）。

语言中的每个元素（标识符）称为串（String）。

字母表 $\Sigma$ 是一个有限的符号集合。

字母表 $\Sigma$ 上的串（$s$）是由 $\Sigma$ 中的符号组成的一个有穷序列。$\epsilon$ 表示空串，其长度 $|\epsilon| = 0$。

在两个串 $x$ 和 $y$ 上可以做连接运算 $xy$，例如：$x=\text{dog}, y = \text{house} \rightarrow xy=\text{doghouse}$。特殊的，$s\epsilon = \epsilon s = s$。

由连接运算可以定义指数运算 $s^i$：

$$\begin{aligned} s^0 &\triangleq \epsilon \\ s^i &\triangleq ss^{i-1}, i>0 \end{aligned}$$

意为自连接 $i$ 次。

语言是给定字母表 $\Sigma$ 上一个任意的可数的串集合。当集合中没有串时，称为空语言 $\varnothing$。

基础图论

基本定义

约定

约定 $G = (V, E)$ 表示点集为 $V$，边集为 $E$ 的图，若无特殊说明，则 $|V| = n$，$|E| = m$。

若干基本定义：

• 边导出子图：选出若干条边，以及这些边所连接的所有顶点组成的图称为边导出子图；
• 点导出子图：选出若干个点，以及两端都在该点集的所有边组成的图称为点导出子图；
• 闭合子图：点集 $V$ 导出的闭合子图是所有 $V$ 可达的点的点导出子图，即：若 $x$ 在子图内，则 $x$ 的所有出边和出点均在子图内的原图子图；等价于每个点能到的所有点都在子图中；
• $k$ 正则图：若一个无向图每个点的度数均为 $k$，则称其为 $k$ 正则图。

DFS 树

当 dfs 一个图时，按照 dfs 的顺序可以构造出一个树结构，被称为 DFS 树。

有向图的 dfs 树主要有四种边：

• 树边：每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
• 反祖边：也叫回边，即指向祖先结点的边。
• 横叉边：在 dfs 树中从一个子树中的结点指向另一个子树中的结点的边，即除了其余三种边的边，表示遇到了一个已经访问过的结点，但这个结点并不是它的祖先。
• 前向边：在 dfs 树中从一个深度小的结点指向一个深度大的结点的边，不包括树边，表示遇到了子树中的结点。

SVM

在线性分类器中，我们知道，线性分类器的任务就是在样本空间中寻找一个超平面，将不同类别的样本分开。但是，对于特定的样本空间，我们可能能够找到很多的超平面都满足条件，那么哪个超平面是最好的呢？

直觉上，我们认为“正中间”的是最好的，它离两类样本都比较远，拥有较好的鲁棒性和泛化能力。

我们已经知道，超平面的方程为 $\boldsymbol{w}^\mathrm T\boldsymbol{x}+b=0$，为了找到“正中间”的超平面，我们要找出两类样本中距离超平面最近的那一个，计算出二者的距离，再将超平面放在中间。

两类样本中距离超平面最近的那个样本直接定义了这个超平面，我们把这几个样本称为“支持向量”：

则两个支持向量之间的距离被称做“间隔”，为

$$\gamma = \dfrac 2{\|\boldsymbol{w}\|}$$

卷积神经网络

卷积神经网络（CNN）是一个专门用于图像处理的神经网络。

从图像分类说起

下面的讨论都是基于假设所有图像的尺寸是固定的，不会突然出现大小不一致的图片。

图像识别模型的输入是一张图片，输出是一个独热（one-hot）的向量 $\hat y$，只有模型认为最有可能的类别为 1，其余都为 0。这个向量的长度表示着当前模型能识别出的种类数目。模型在输出独热向量之前，会先通过 Softmax 输出一个向量 $y'$，我们希望 $y'$ 和 $\hat y$ 的交叉熵尽可能地小。

对于输入，人眼看到的是一张三维的图像，计算机看到的是什么呢？计算机看到的是一个三维的张量（粗略的认为是维度大于 2 的矩阵），一维代表图片的宽，一维代表图片的高，另一维代表这张图片通道的个数，当给定一张彩色图片时，图片通道数为 3，分别表示 R、G 和 B。

当我们把一张图片“拉直”成一个向量之后，就可以放到神经网络中让它进行识别分类了。

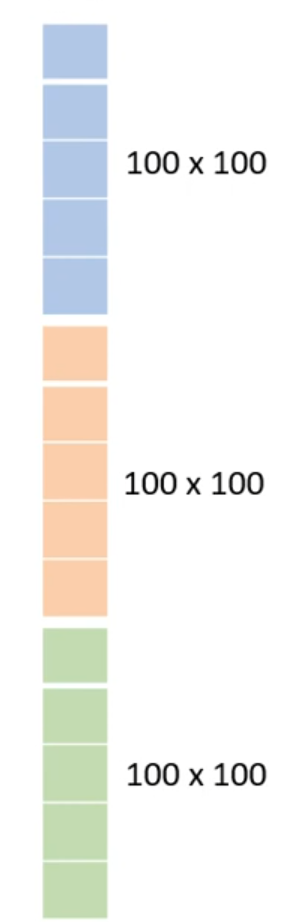
目前为止，我们只学到了全连接神经网络，如果输入是一个 $100\times100\times3$ 的向量，第二层的神经元有 1000 个，那么将会有 $3 \times 10^7$ 个权重，这是一个非常巨大的数，计算过程会非常缓慢，同时过拟合的风险也会增加。

考虑图像识别的特性，我们并不需要每一个神经元和输入的每一维都有一个权重，即全连接是不必要的。

Softmax Regression

简介

Softmax 回归模型属于有监督学习，是逻辑回归模型在多分类问题上的推广，其类标签 $y$ 可以取两个以上的值。

由于我们要解决的是多分类问题，类标签 $y$ 可以取 $k$ 个不同的值，因此对于训练集 $\left\{(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \dots, (x^{(m)}, y^{(m)})\right\}$，我们有 $y^{(i)} \in \left\{1, 2, \dots, k\right\}$。

对于给定的测试输入 $x$，我们希望用假设函数针对每一个类别 $j$ 都估算出一个概率值 $p(y = j \mid x)$，表示 $x$ 数据第 $j$ 类的概率。因此，我们的假设函数将要输出一个 $k$ 维的向量（向量元素的和为 1）来表示这 $k$ 个估计的概率值。

假设函数 $h_\theta(x)$ 形式如下：

$$h_\theta\left(x^{(i)}\right) = \begin{bmatrix} p(y^{(i)}=1 \mid x^{(i)};\theta \\ p(y^{(i)}=2 \mid x^{(i)};\theta \\ \vdots \\ p(y^{(i)}=k \mid x^{(i)};\theta) \end{bmatrix} = \dfrac{1}{\sum_{j=1}^k e^{\theta_j^\mathrm Tx^{(i)}}} \begin{bmatrix} e^{\theta_1^\mathrm Tx^{(i)}} \\ e^{\theta_2^\mathrm Tx^{(i)}} \\ \vdots \\ e^{\theta_k^\mathrm Tx^{(i)}} \end{bmatrix}$$

其中 $\theta_1, \theta_2, \cdots, \theta_k \in \mathbb{R}^{n+1}$ 是模型的参数，$\dfrac{1}{\sum_{j=1}^k e^{\theta_j^\mathrm Tx^{(i)}}}$ 是为了将所有的概率分布进行归一化，使所有概率之和为 1。

为了方便起见，我们令

$$\boldsymbol{\theta} = \begin{bmatrix} \theta_1^\mathrm T \\ \theta_2^\mathrm T \\ \vdots \\ \theta_k^\mathrm T \end{bmatrix}_{k \times (n + 1)}$$