Logistic Regression

Logistic Regression

逻辑回归可以用来处理离散标签分类的问题，如二分类、三分类 $\cdots$ $n$ 分类等。

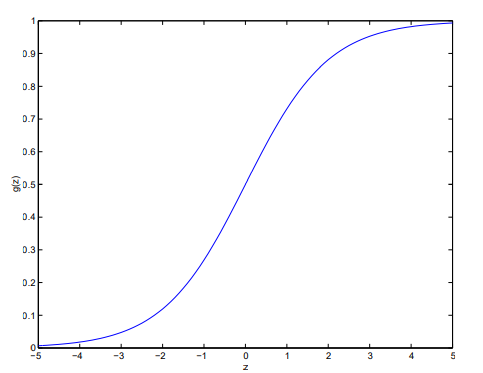
由于在分类时我们不希望得到连续的值，而只得到两类离散值，如 $0$、$1$，我们引入 Sigmoid 函数（也称为 Logistic 函数）：

$$g(x) = \dfrac{1}{1+e^{-x}}$$

可以发现，$g(x) \in (0,1)$，$g(0) = \dfrac 12$，且 $\lim\limits_{x \to -\infty}g(x) = 0$，$\lim\limits_{x\to +\infty}g(x)=1$。

与线性回归类似地，我们定义回归函数为 $F_{\vec w, b}(\vec x) = \vec w \cdot \vec x + b$，与 Sigmoid 函数结合，就得到了逻辑回归模型 $f_{\vec w, b}(\vec x) = g(\vec w \cdot \vec x + b)=g\left(\sum\limits_{i=0}^nw_ix_i+b\right)$。

对于逻辑回归模型，它所做的是输入一个（组）特征 $x$，输出一个 0 到 1 之间的数字。

Interpretation of logistic regression output

我们将 $F_{\vec w, b}(\vec x)$ 的输出看做给定某个输入 $x$ 的分类 $y$ 等于 1 的概率。

例如令 $x$ 为“肿瘤大小”，$y$ 为 0（良性肿瘤）或 1（恶性肿瘤），则 $F(x) = 0.7$ 表示该病人的肿瘤有 $70\%$ 的概率为恶性肿瘤。由于我们此处只做二分类，故 $P(x=0)+P(x=1)=1$，即病人的肿瘤有 $30\%$ 的概率为良性肿瘤。

有时会见到如下的记号：$f_{\vec w, b}(\vec x) = P(y = 1\mid \vec x;\vec w;b)$，这表示这个函数是在具有参数 $\vec w$ 和 $b$ 的情况下，给定特征 $\vec x$，计算 $y = 1$ 的概率的函数。

Decision Boundary

由于 Sigmoid 函数会输出一个连续值，如 0.3、0.7等，我们必须要确定一个阈值，使得超过这个阈值的特征分类为 1，低于这个阈值的特征分类为 0. 常见地，我们把这个阈值确定为 0.5，即若 $f(x) \geq 0.5$，也即 $\vec w \cdot \vec x + b \geq 0$ 时 $\hat{y} = 1$。

我们来看一个例子：

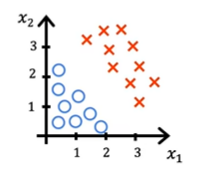
在这个例子中，红色叉代表 $y=1$，蓝色圈代表 $y=0$，$f_{\vec w, b}(\vec x) = g(w_1x_1+w_2x_2+b)$，在此例子中，我们令 $w_1=1,\ w_2=1,\ b=-3$，我们关心的是直线 $\vec w \cdot \vec x + b = 0$，在此例中为 $x_1+x_2=3$，其恰好将数据划分为两部分，在直线左侧的属于为 $y=0$，右侧的为 $y=1$。我们将这条直线称为决策边界（Decision Boundary）。

显然，当参数选择不同时，决策边界也是不同的。

Non-linear decision boundaries

我们来看一个更复杂的例子：

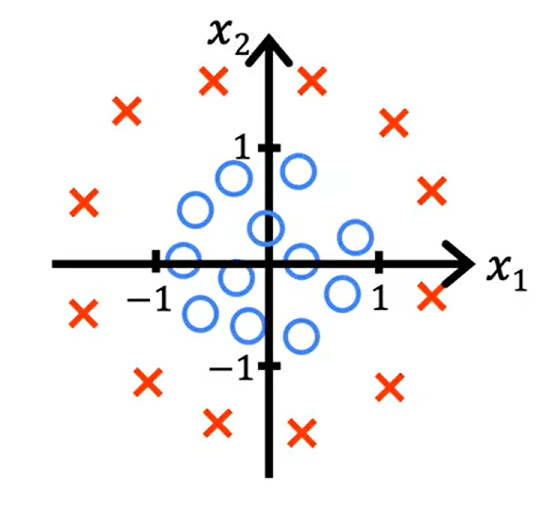
本例中，容易发现，决策边界将不再是一条直线。我们令 $z = w_1x_1^2+w_2x_2^2+b$，此时 $f_{\vec w, b}(\vec x) = g(z) = g(w_1x_1^2+w_2x_2^2+b)$。假设我们令 $w_1=w_2=1,\ b=-1$，则 $z=x_1^2+x_2^2-1$，则决策边界为 $z=0 \Longrightarrow x_1^2+x_2^2=1$。

对于更麻烦的决策边界，我们可以考虑用更高维的多项式来表达，根据插值法我们知道，如果一条曲线经过了 $n$ 个点，则必定存在一个 $n - 1$ 次的多项式与之对应。

对于插值，我们可以使用 Lagrange 插值 or Newton 插值，此处略去。

Cost Function

在线性回归中，代价函数表示为

$$J(\theta) = \dfrac 1m \sum\limits_{i = 1}^m\dfrac 12 \left(h_\theta(x^{(i)}) - y^{(i)}\right)^2$$

普适地，我们将式子改写为

$$J(\theta) = \dfrac 1m \sum\limits_{i = 1}^m\operatorname{Cost}\left(h_\theta(x^{(i)}), y^{(i)}\right)$$

其中 $\operatorname{Cost}\left(h_\theta(x^{(i)}), y^{(i)}\right) = \dfrac 12 \left(h_\theta(x^{(i)}) - y^{(i)}\right)^2$，即 $\dfrac 12$ 倍的平方误差。

注意到上标 $(i)$ 均对应实际数据，于是可以全部除去，即 $\operatorname{Cost}\left(h_\theta(x), y\right) = \dfrac 12 \left(h_\theta(x) - y\right)^2$。

代价函数表示的是预测值 $h_\theta(x)$ 与实际值 $y$ 不符时，预测模型需要付出的代价。由于我们希望预测模型预测的结果与实际值尽可能接近，于是我们要让代价函数得到的值尽可能小。

这个函数在线性回归中很好用，但在 Logistic 回归中需要进行一些改变。如果在 Logistic 回归中使用这个代价函数，则代价函数 $J(\theta)$ 会变成一个关于 $\theta$ 的非凸函数，这将使得我们无法使用梯度下降法求得 $\theta$ 的值。

此处的非凸函数有一种可能，是有多个局部最小值的函数，这使得我们难以找到全局最小值。

于是我们希望找到一个新的代价函数，使得它是凸函数，如此我们便可以通过梯度下降法找到全局最小值。

我们将 Logistic 回归的 Cost Function 定义如下：

$$\operatorname{Cost}(h_\theta(x), y) = \begin{cases}-\log(h_\theta(x)),\ &\text{if y = 1} \\ -\log(1 - h_\theta(x)),\ &\text{if y = 0}\end{cases}$$

这个函数事实上是一个惩罚函数，用于惩罚回归模型得到的预测值与真实值的差距，预测值越离谱，惩罚越重。例如当 $y = 1$ 时，如果模型得到的预测值为 $0$，则它将受到 $-\log 0 = +\infty$ 的惩罚。

由于标签值 $y$ 只会等于 0 或 1，于是我们可以把分段函数化简为一个：

$$\operatorname{Cost}(h_\theta(x), y) = -y\log(h_\theta(x)) - (1 - y)\log(1 - h_\theta(x))$$

通过这个这个代价函数，我们可以得到 Logistic 回归的代价函数：

$$J(\vec\theta) = -\dfrac 1m\sum\limits_{i = 1}^m\left[y^{(i)}\log h_\theta(x^{(i)}) + (1 - y^{(i)})\log(1 - h_\theta(x^{(i)}))\right]$$

这个式子称为对数似然损失函数，是从统计学中的极大似然法得到的，是统计学中为不同模型快速寻找参数的办法。

我们在此处将一组 $\theta$ 值 $\left(\theta_0, \theta_1, \theta_2, \dots, \theta_n\right)$ 写作一个向量 $\vec\theta$ 以便于函数式的计算与化简。

我们希望找到一个 $\vec\theta$，使得 $J(\vec\theta)$ 取得最小值。对于给定的要求预测的 $x$，我们需要输出预测 $h_\theta(x)=\dfrac 1{1 + e^{-\vec\theta^Tx}}$，这个输出即为在输入为 $x$，参数为 $\vec\theta$ 时 $y=1$ 的概率，记作 $p(y = 1 \mid x;\ \vec\theta)$。

Gradient Decent

下面我们通过梯度下降法最小化 $J(\vec\theta)$。梯度下降法的基本模板为：

不断执行

$$\theta_j = \theta_j - \alpha \dfrac{\partial}{\partial \theta_j} J(\vec\theta)$$

直到 $\theta_j$ 收敛。

在 $n = 1$ 时，梯度下降的式子为：

Repeat
{
$\ \ \ \theta_0 := \theta_0 - \alpha \dfrac 1m\sum\limits_{i = 1}^m\left(h_\theta\left(x^{(i)}\right) - y^{(i)}\right)$
$\ \ \ \theta_1 := \theta_1 - \alpha \dfrac 1m\sum\limits_{i = 1}^m\left(h_\theta\left(x^{(i)}\right) - y^{(i)}\right)x^{(i)}$
}

在 $n > 1$ 时，梯度下降的式子将会有所变动：

Repeat
{
$\ \ \ \theta_j := \theta_j - \alpha \dfrac 1m\sum\limits_{i = 1}^m\left(h_\theta\left(x^{(i)}\right) - y^{(i)}\right)x_j^{(i)}$
}

其中 $\dfrac 1m\sum\limits_{i = 1}^m\left(h_\theta\left(x^{(i)}\right) - y^{(i)}\right)x_j^{(i)}$ 即为代价函数 $J(\vec\theta)$ 对 $\theta_j$ 的偏导。

事实上 $n=1$ 的式子与 $n > 1$ 的式子本质上是相同的，因为我们约定 $x_0 = 1$，于是 $\theta_0$ 的梯度下降式本质上也满足

$$\theta_j := \theta_j - \alpha \dfrac 1m\sum\limits_{i = 1}^m\left(h_\theta\left(x^{(i)}\right) - y^{(i)}\right)x_j^{(i)}$$

这个梯度下降式。

Multi-class classification 1vsAll

“一对多”方法：先确定一类，其余的认为是一类，不断分类即可得到所有类别。

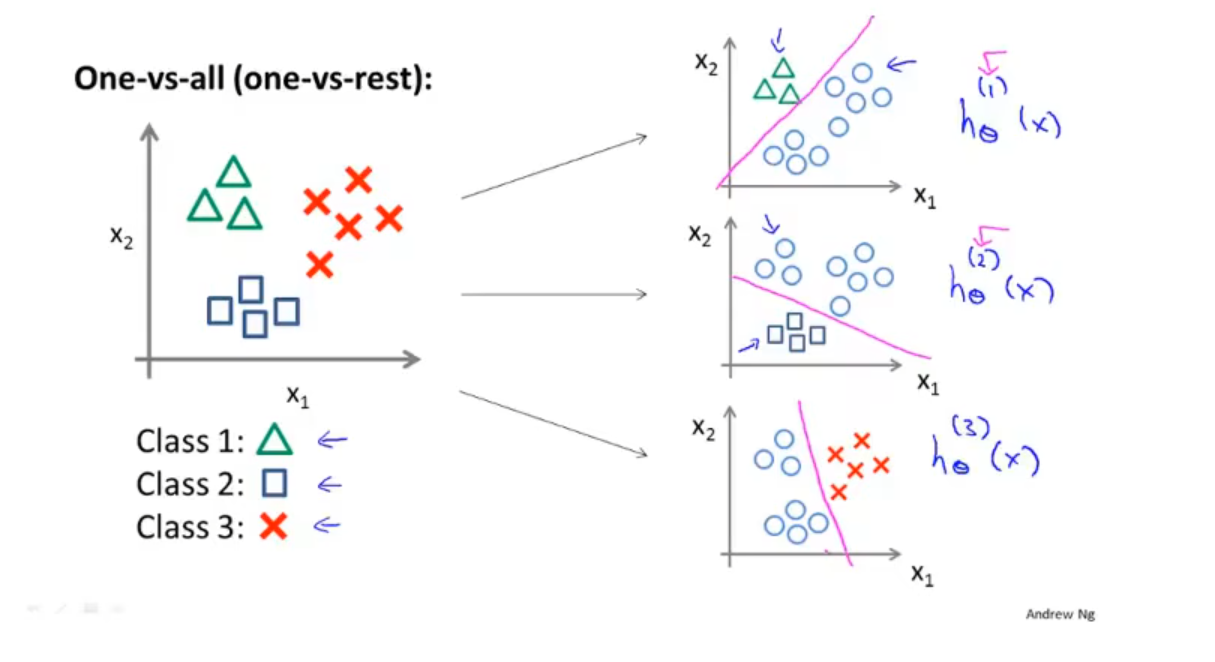
对于此例，我们拟合出三个分类器 $h_\theta^{(i)} = P(y = i \mid x;\ \theta), (i = 1, 2, 3)$，尝试估计出当给定 $x$ 和 $\theta$ 时 $y = i$ 的概率。

对于类别数为 $m$ 的数据集，我们构造 $m$ 个分类器，第 $i$ 个分类器可以分出第 $i$ 类数据；对于一个输入，只需找到输出最大的那个分类器，并将其对应的类别作为输入的类别。