Neural Networks

Neural Networks

---

Non-linear hypotheses

在特征较少时，对于一个边界较为复杂的数据集中，我们可以使用逻辑回归，通过构造一个多项式来拟合决策边界，但在特征较多时，逻辑回归便显得较为繁杂，我们很难构造一个合适的多项式来较好的拟合其决策边界。

例如，当有 100 个特征时，如果我们只构造一个二次多项式，那么这个多项式最多会有 $\binom{100}{2}$ 个，也就是说，二次项会有 $\mathcal{O}(n^2)$ 个，极易导致过拟合的情况出现，同时也会出现计算量过大的问题。

如果我们继续将多项式的次数提高，那么会有 $\mathcal{O}(n^3)$ 个三次项，$\mathcal{O}(n^4)$ 个四次项……这对我们的模型构造和计算都是不可承受的。

考虑一个计算机视觉中的问题：如何让计算机识别出一辆汽车？人眼对于识别一辆汽车轻而易举，但对于计算机，它得到的可以是一个亮度的矩阵，也可以是一个颜色的矩阵等等。

在训练这样的模型时，我们需要做的是提供两个带标签的数据集，其中一个表示这里面的数据全都是车，另一个表示全都不是车。在分类器训练完成后，如果给定一个汽车的图片并要求它分类，理想状态下分类器可以识别出这是一辆汽车。

具体地，我们假设在每个图片的相同位置取两个像素点，并将其传入分类器中，如下图所示：

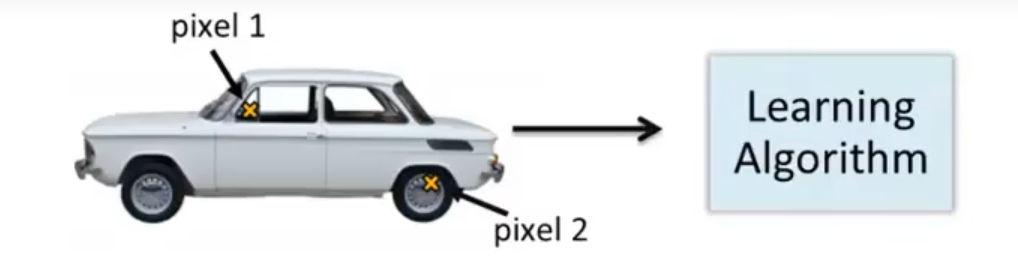
对于是汽车的样本和不是汽车的样本，我们可以发现，存在一个非线性的决策边界使得这两类可以被分开：

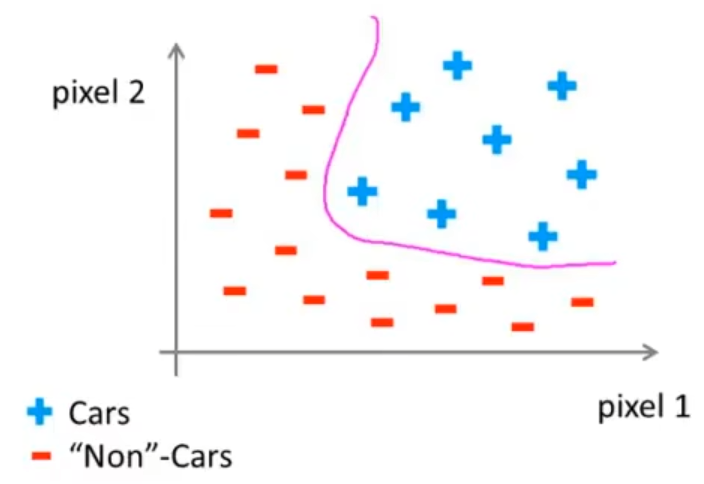
现在我们考虑每个样本的特征数量，假设每个样本都是一张 $50 \times 50$ 的图片，那么就有 2500 个像素点，特征数量 $n = 2500$，这是在只使用灰度图片的情况下，如果我们使用彩色图片，这个数字将会变为 $2500 \times 3 = 7500$。
此时如果使用逻辑回归的话极大可能会出现过拟合的问题，这就引出了我们的神经网络模型。

---

Model representation

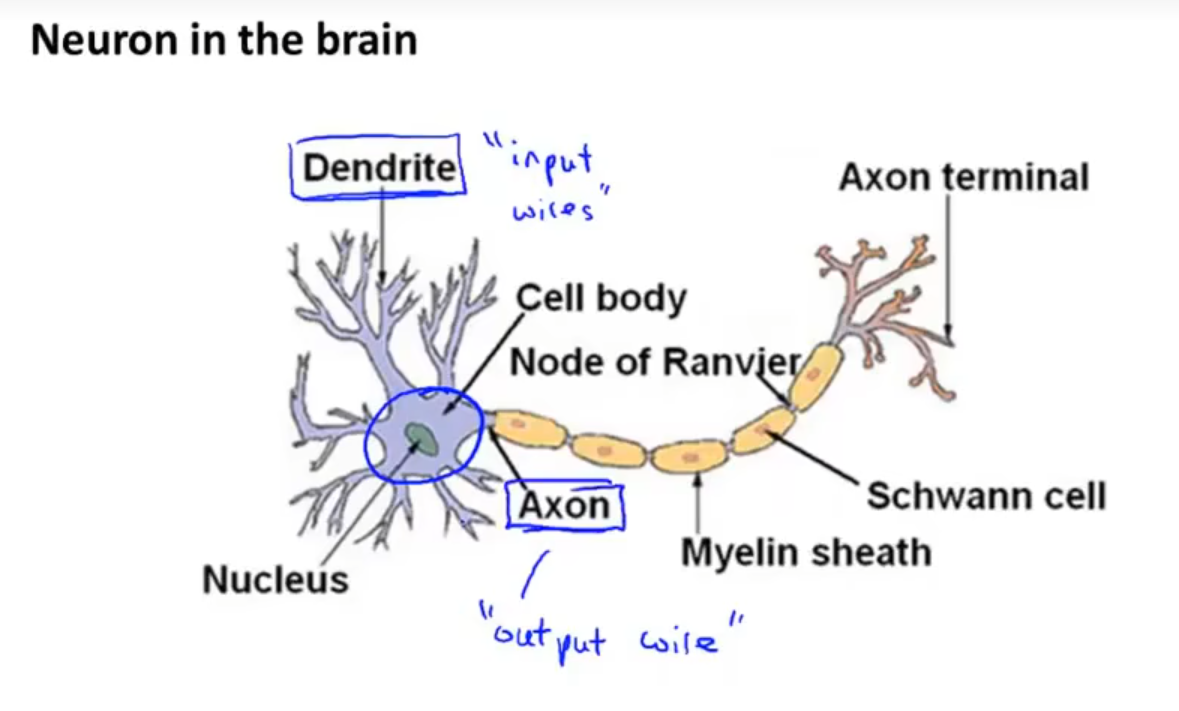
可以认为一个神经元是通过树突接收信号，进行一系列计算后通过轴突输出信号。

最简单的一个神经元模型如图所示：

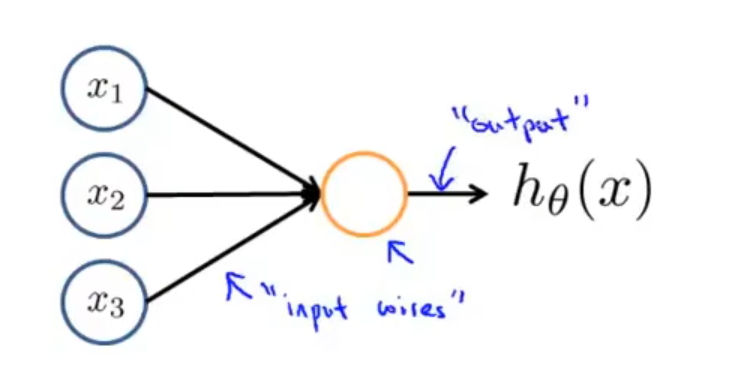
这表示有三个输入，通过神经元计算出 $h_\theta(x) = \dfrac 1{1 + e^{-\theta^Tx}}$ 的值并输出。此处的 $h_\theta(x)$ 被称为 Sigmoid 激活函数，$\theta$ 一般被称作权重或参数。注意，有时也会加上一个输入 $x_0$，被称作偏置单元，但由于其值永远为 0，故可以省略。

神经网络实际上是一组神经元连接在一起的集合。

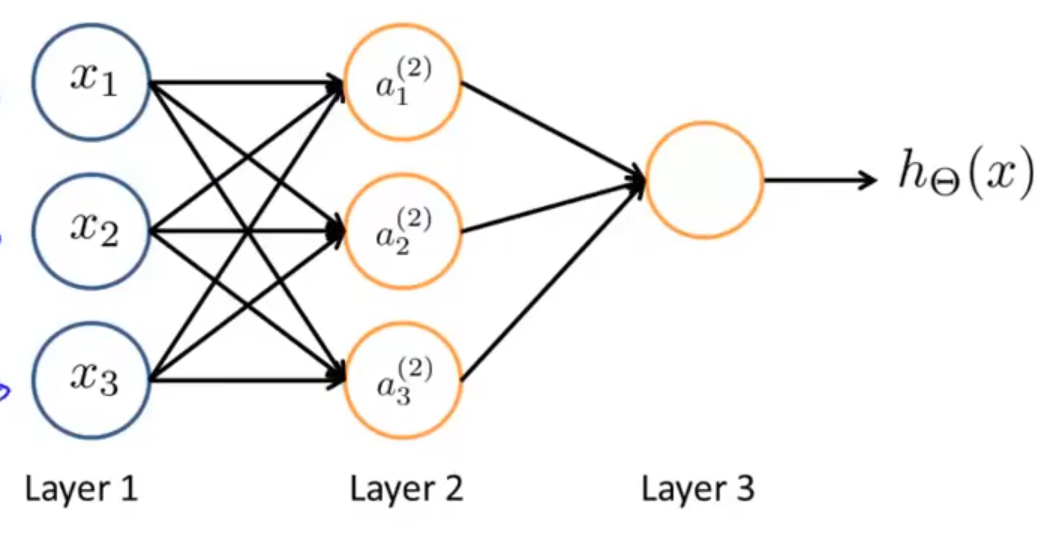
第一层被称作输入层，最后一层被称作输出层，中间的第二层被称作隐藏层，隐藏层可以不止一层，非输入层和输出层的层都被称为隐藏层。

下面对神经网络中一些记号进行解释：

• $a_i^{(j)}$ 表示第 $j$ 层第 $i$ 个神经元或单元的激活项，激活项是指由一个具体的神经元计算并输出的值；
• $\Theta^{(j)}$ 表示控制从第 $j$ 层到第 $j+1$ 层的映射的权重矩阵。

对于此图所表示的神经网络，几个激活项的值分别为：

$$a_1^{(2)} = g\left(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3\right)$$

$$a_2^{(2)} = g\left(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3\right)$$

$$a_3^{(2)} = g\left(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3\right)$$

$$h_\Theta(x) = a_1^{(3)} = g\left(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)}\right)$$

其中，$g(x)=\dfrac{1}{1+e^{-x}}$ 为 sigmoid 函数。如果第 $j$ 层有 $s_j$ 个单元，$j+1$ 层有 $s_{j+1}$ 个单元，则 $\Theta^{(j)}$ 的维数为 $s_{j+1} \times (s_j + 1)$。

通过观察上面 $a_1^{(2)}$、$a_2^{(2)}$ 和 $a_1^{(2)}$ 三式，我们不难将其写做一个矩阵相乘的形式：

$$g\left(\begin{bmatrix}x_0 \\ x_1 \\ x_2 \\ x_3\end{bmatrix} \times \begin{bmatrix}\Theta_{10} & \Theta_{11} & \Theta_{12} & \Theta_{13} \\ \Theta_{20} & \Theta_{21} & \Theta_{22} & \Theta_{23}\\ \Theta_{30} & \Theta_{31} & \Theta_{32} & \Theta_{33}\end{bmatrix}^{\mathrm{T}}\right) = \begin{bmatrix}a_1 \\ a_2 \\ a_3\end{bmatrix}$$

上式也可写作：$z^{(2)} = \Theta^{(1)}x\quad a^{(2)}=g\left(z^{(2)}\right)$

如果把输入 $x$ 看做是第一层的激活项 $a^{(1)}$，则整个式子可以写作

$$\begin{cases}z^{(i+1)} = \Theta^{(i)}a^{(i)} \\ a^{(i+1)} = g\left(z^{(i+1)}\right)\end{cases}$$

注意，这其中的偏置单元 $a_0$ 本身不会在输入中给出，一般默认其为 $1$。
设输出层为第 $n$ 层，则$h_\Theta(x) = a^{(n)} = g\left(z^{(n)}\right)$，这个计算过程被称为前向传播。

在神经网络中，信息从上一个神经元直接流转到下一个神经元，直到输出，依据每一个神经元的输入并根据相应规则可以计算出输出，最终得到在当前参数下的损失函数的过程，称为前向传播。

这个神经网络相当于一个多层的逻辑回归模型，其将上一层数据的逻辑回归结果作为输入传入下一层中。

---

Example and intuitions

考虑一个异或问题，其中输入特征为 $x_1$，$x_2$ 两个，其取值只能为 $0$ 或 $1$，则正样本和负样本的分布如下图所示：

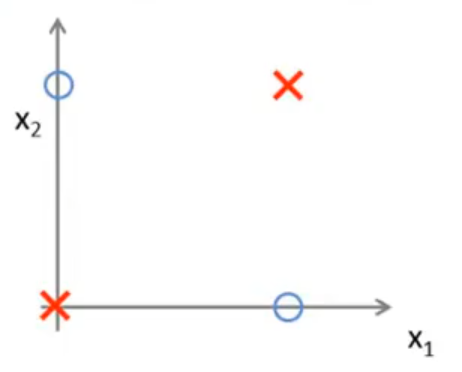
对于该分类问题，预测函数显然为 $y = x_1 \bigoplus x_2$，其中 $\bigoplus$ 表示异或，但我们希望构造一个神经网络，显然神经网络中我们是无法使用异或运算的，于是我们考虑构造一个非线性函数来拟合异或的结果。

首先，我们考虑构造一个能进行 $\operatorname{AND}$ 运算的神经元，

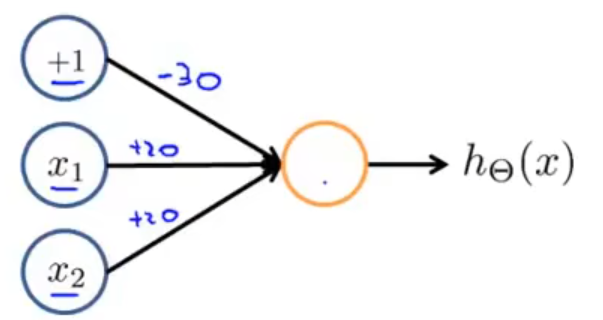
对于该神经元，我们得到的输出 $h_\Theta(x) = g\left(20x_1 + 20x_2 - 30\right)$，我们没有显式的给出权重矩阵 $\Theta$，但把每个单元对应的权重标在了图中。事实上，此处的权重并不一定要取这三个值，只需要保证最后得到的结果正确即可。下表展示了该神经元的计算结果：

$x_1$	$x_2$	$h_\Theta(x)$
$0$	$0$	$g(-30) \approx 0$
$0$	$1$	$g(-10) \approx 0$
$1$	$0$	$g(-10) \approx 0$
$1$	$1$	$g(10) \approx 1$

通过上表我们可以得到 $h_\Theta(x) \approx x_1 \operatorname{AND} x_2$。

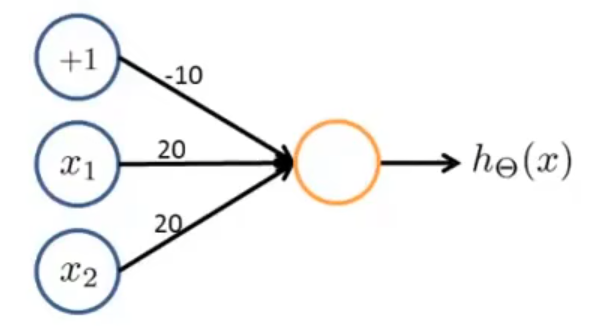
此神经元实现了 $\operatorname{OR}$ 的功能，计算结果略去。

接下来我们考虑如何实现一个计算 $x_1 \operatorname{XNOR} x_2$（同或）的神经网络。

考虑逻辑推导同或，由于 $A \bigoplus B = \overline A B + A \overline B$，由德摩根律得 $A \operatorname{XNOR} B = \overline{\left(\overline A B + A \overline B\right)} = \overline{AB} + AB$。

根据此，我们可以构造一个神经网络：

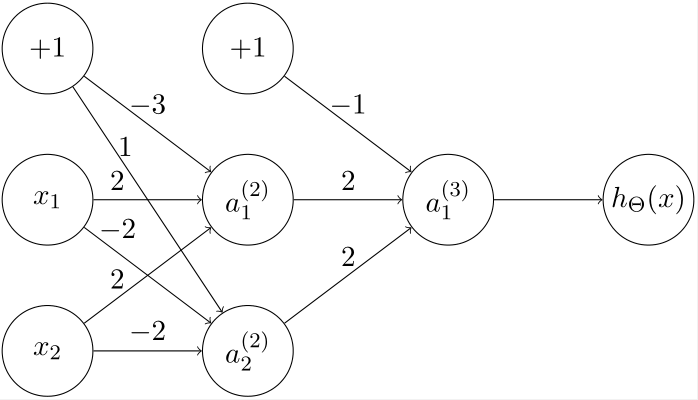
通过简单的计算我们得到，$a_1^{(2)}$ 计算得到的结果是 $AB$，$a_2^{(2)}$ 计算得到的结果是 $\overline{AB}$，$a_1^{(3)}$ 计算得到的结果是 $\overline{AB} + AB$，是我们需要的结果。

---

Multi-class classification

多分类问题可以将其看做一个一对多方法的拓展。

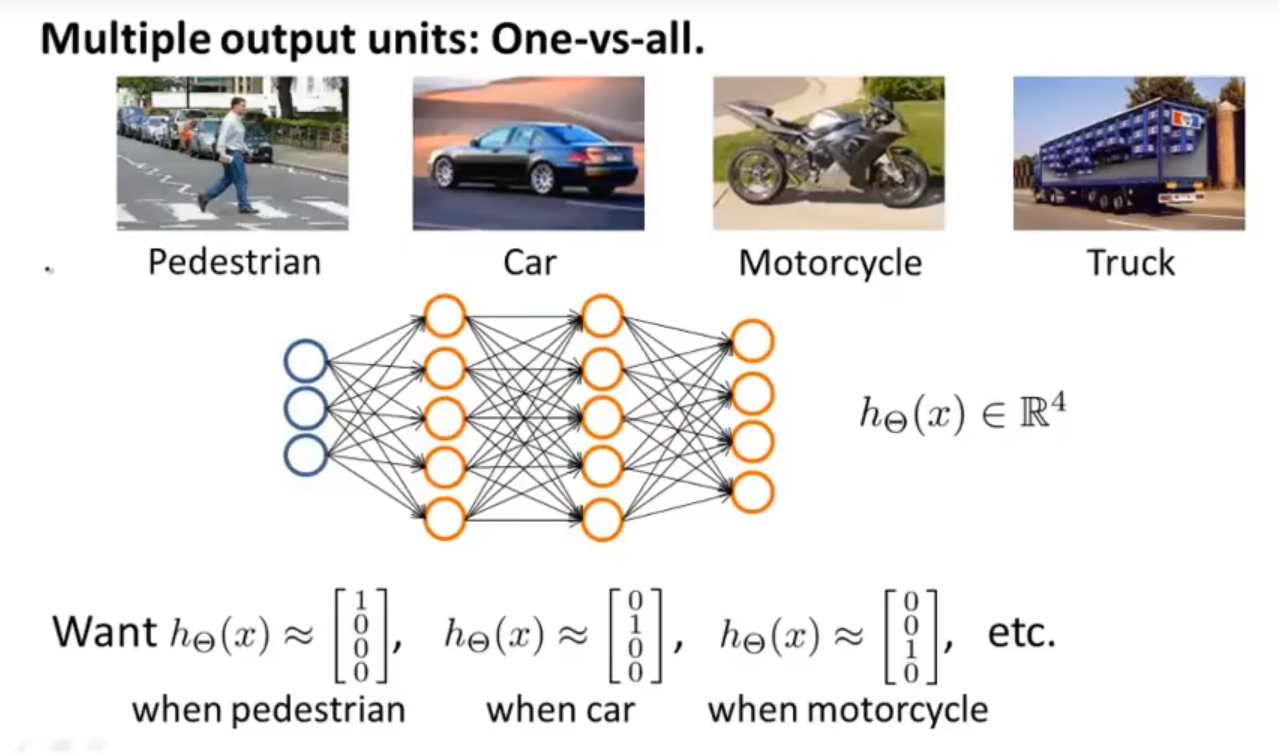
对于上例，我们构造了一个输出层有四个神经元的神经网络，则神经网络的输出将会是一个含有四个数的向量 $h_\Theta(x) \in \mathbb{R}^4$，当数据分别属于不同的类别时，我们希望其能激活不同的输出单元来表示预测的结果，这与逻辑回归中的一对多法非常类似。

此时训练集可表示为 $\left\{\left(x^{(1)}, \vec y^{(1)}\right), \left(x^{(2)}, \vec y^{(2)}\right), \dots, \left(x^{(m)}, \vec y^{(m)}\right) \right\}$，其中 $x^{(i)}$ 表示一张图片，$\vec y^{(i)} \in \mathbb{R}^4$ 表示一个四维向量，用来表示每张图片所属的类别。

---

Cost function

下面用 $L$ 表示神经网络中的总层数，$s_l$ 表示第 $l$ 层中不包括偏置单元的单元个数。

• 对于一个二分类问题，输出单元只有一个，输出结果 $h_\Theta(x) \in \mathbb{R}$，$s_L = 1$，为了方便，也可以令 $K$ 为输出层的单元数目，在此类问题中，$K = 1$。
• 对于一个多分类问题，假设需要分为 $K$ 类，则输出单元有 $K$ 个，输出结果 $h_\Theta(x) \in \mathbb{R}^K$，$s_L = K$，注意，一般而言 $K \geq 3$，由于一个二分类问题使用一个输出单元即可，而不使用 $\mathbb{R}^2$ 的向量表示。

在逻辑回归中，我们使用的代价函数为

$$J(\theta) = -\dfrac 1m \left[\sum\limits_{i=1}^m{y^{(i)} \log h_\theta(x^{(i)}) + (1 - y^{(i)})\log(1 - h_\theta(x^{(i)}))}\right] + \dfrac \lambda{2m}\sum\limits_{j=1}^n{\theta_j^2}$$

在神经网络中，代价函数基本一致，不同的是由于参数不再是一个向量，而是一个矩阵，于是代价函数会有所变动。

具体地，假设 $h_\Theta(x) \in \mathbb{R}^K$，$\left(h_\Theta(x)\right)_i$ 表示神经网络中输出向量的第 $i$ 个输出，即向量中的第 $i$ 项，则代价函数表示为

$$\begin{aligned} J(\Theta) = &-\dfrac 1m\left[\sum\limits_{i=1}^m{\sum\limits_{k=1}^K{y_k^{(i)}\log (h_\Theta(x^{(i)})_k) + (1 - y_k^{(i)}) \log (1 - (h_\Theta(x^{(i)}))_k)}}\right] \\ &+ \dfrac \lambda{2m}\sum\limits_{l=1}^{L-1}{\sum\limits_{i=1}^{s_l}{\sum\limits_{j=1}^{s_{l+1}}\left(\Theta_{ji}^{(l)}\right)^2}} \end{aligned}$$

对于此函数，直观的理解是将其与逻辑回归的代价函数做对比，由于神经网络中输出是一个 $\mathbb{R}^K$ 的向量，于是必须存在一个求和将这些输出单元的代价加起来，这就有了内层的求和号；

对于第 $k$ 个输出单元，它预测的类别是 $h_\Theta(x^{(i)})_k$，实际的类别是 $(y^{(i)})_k$，将其在逻辑回归的代价函数中做替换即可得到神经网络代价函数中的前一项；

而后一项明显为 L2 正则项，逻辑回归中是将除 $\theta_0$ 以外的所有参数平方后求和，类比到神经网络中，以 $a_1^{(i+1)}$ 举例，它会和 $a_1^{(i)}, a_2^{i}, \dots, a_{s_{i}}^{(i)}$ 这 $s_{i}$ 个神经元相连，相连时的参数分别为 $\Theta_{11}^{(i)}, \Theta_{12}^{(i)}, \dots, \Theta_{1s_i}^{(i)}$，那么这个神经元表示的逻辑回归即为

$$a_1^{(i+1)} = \sum\limits_{j=0}^{s_i}{\Theta_{1j}^{(i)}a_j^{(i)}}$$

那么这一个逻辑回归对应的 L2 正则项为

$$\sum\limits_{j=1}^{s_i}\left({\Theta_{1j}^{(i)}}\right)^2$$

将第 $i+1$ 层的 $s_{i+1}$ 个神经元都考虑进来得到

$$\sum\limits_{j=1}^{s_i}{\sum\limits_{k=1}^{s_{i+1}}\left({\Theta_{kj}^{(i)}}\right)^2}$$

再把第 $1$ 层到第 $L-1$ 层考虑进来便得到神经网络代价函数中的后一项。

---

Backpropagation algorithm

反向传播算法是一个让代价函数最小化的算法。在上一节中，我们得到了神经网络的代价函数 $J(\Theta)$，本节我们要做的是

$$\underset{\Theta}{\arg \min}\ J(\Theta)$$

为了使用梯度下降法来找到这个最小值，我们需要计算 $J(\Theta)$ 和 $\dfrac{\partial}{\partial \Theta_{ij}^{(l)}}J(\Theta)$ 的值，从而能够使用梯度下降。

反向传播的微积分原理

先从一个最简单的神经网络看起：每一层只有一个神经元，假设这个神经网络有四层，那么就会有三个权重 $\omega_1, \omega_2, \omega_3$ 和三个偏置值 $b_1, b_2, b_3$。

先考虑最后两个神经元 $a^{(L)}$ 和 $a^{(L-1)}$，且给定一个训练样本，目标值为 $y$，那么这个神经网络对于该样本的代价为 $C_0 = \dfrac 12\left(a^{(L)} - y\right)^2$。

考虑最后一层的激活值是如何计算的：

$$a^{(L)} = g\left(\omega^{(L)}a^{(L-1)} + b^{(L)}\right)$$

其中 $g(x)$ 为 Sigmoid 函数。不妨给 $\omega^{(L)}a^{(L-1)} + b^{(L)}$ 取一别名 $z^{(L)}$，于是原式成为

$$a^{(L)} = g\left(z^{(L)}\right)$$

这个过程如下图所示：

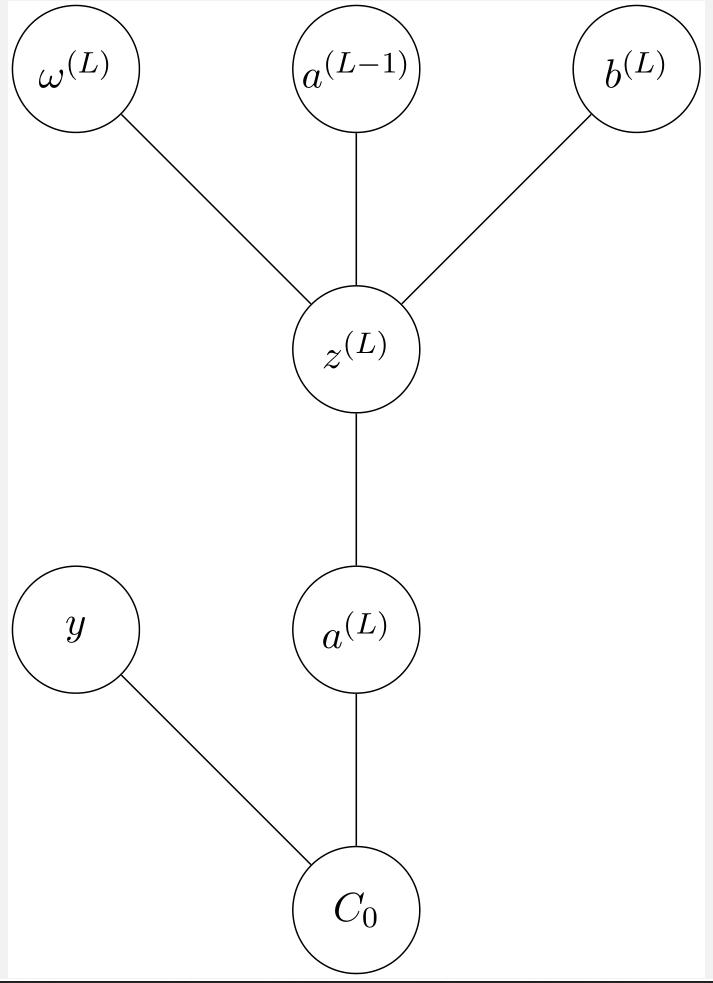
当然，$a^{(L-1)}$ 是根据上一层的权重和偏置值得到的，此处不再画出。

现在，我们考虑计算当 $\omega^{(L)}$ 变化时，代价函数的变化程度，即

$$\dfrac{\partial}{\partial \omega^{(L)}} C_0$$

由于 $\omega^{(L)}$ 会首先导致 $z^{(L)}$ 的变化，再导致 $a^{(L)}$ 的变化，我们把上式拆开，根据求导的链式法则得到

$$\dfrac{\partial}{\partial \omega^{(L)}} C_0 = \dfrac{\partial z^{(L)}}{\partial \omega^{(L)}} \cdot \dfrac{\partial a^{(L)}}{\partial z^{(L)}} \cdot \dfrac{\partial C_0}{\partial a^{(L)}}$$

下面计算右侧各式的值：

$$\begin{aligned} \dfrac{\partial C_0}{\partial a^{(L)}} &= \dfrac{\partial }{\partial a^{(L)}} \dfrac 12 \left(a^{(L)} - y\right)^2= \left(a^{(L)} - y\right) \\ \\ \dfrac{\partial a^{(L)}}{\partial z^{(L)}} &= \dfrac{\partial}{\partial z^{(L)}} g\left(z^{(L)}\right)= \dfrac{\partial}{\partial z^{(L)}} z^{(L)} \cdot g'\left(z^{(L)}\right) = g'\left(z^{(L)}\right) \\ \\ \dfrac{\partial z^{(L)}}{\partial \omega^{(L)}} &= \dfrac{\partial}{\partial \omega^{(L)}} \left(\omega^{(L)}a^{(L-1)} + b^{(L)}\right) = a^{(L-1)} \end{aligned}$$

于是

$$\dfrac{\partial}{\partial \omega^{(L)}} C_0 = a^{(L-1)}g'\left(z^{(L)}\right)\left(a^{(L)} - y\right)$$

总的代价函数为许多训练样本所有代价的平均，则有

$$\dfrac{\partial}{\partial \omega^{(L)}}C = \dfrac 1n \sum\limits_{k=0}^{n-1}{\dfrac{\partial}{\partial \omega^{(L)}}C_k}$$

而这只是梯度向量

$$\nabla C = \begin{bmatrix}\frac{\partial C}{\partial \omega^{(1)}} \\ \\ \frac{\partial C}{\partial b^{(1)}} \\ \\ \vdots \\ \\ \frac{\partial C}{\partial \omega^{(L)}} \\ \\ \frac{\partial C}{\partial b^{(L)}}\end{bmatrix}$$

的其中一个分量，我们还需要求出代价函数对于偏置值的偏导数，而这只需要将上式中的 $\frac{\partial z^{(L)}}{\partial \omega^{(L)}}$ 改为 $\frac{\partial z^{(L)}}{\partial b{(L)}}$ 即可，显然此值为 $1$，于是

$$\dfrac{\partial C_0}{\partial b^{(L)}} = 1g'\left(z^{(L)}\right)\left(a^{(L)} - y\right)$$

我们再来看代价函数对上一层的激活值的敏感度

$$\dfrac{\partial C_0}{\partial a^{(L-1)}} = \omega^{(L)}g'\left(z^{(L)}\right)\left(a^{(L)} - y\right)$$

虽然我们不能直接修改权重，但我们可以通过此来判断代价函数对之前的权重和偏置值的敏感度。

---

现在来考虑多个神经元的情况。我们令 $j$ 表示最后一层的第 $j$ 个神经元，$k$ 表示倒数第二层的第 $k$ 个神经元，此时最后一层的代价为

$$C_0 = \dfrac 12 \sum\limits_{j=0}^{s_L-1}{\left(a_j^{(L)} - y_j\right)^2}$$

再次提醒，$\omega^{(L)}_{jk}$ 表示 $L - 1$ 层的第 $k$ 个神经元连向 $L$ 层的第 $j$ 个神经元的权重，与单神经元类似地，令

$$z_j^{(L)} = \sum\limits_{k=0}^{s_{L-1}-1} {\omega_{jk}^{(L)}a_k^{(L-1)}} + b_j^{(L)}$$

则最后一层的激活值为

$$a_j^{(L)} = g\left(z_j^{(L)}\right)$$

其中 $g(x)$ 为 Sigmoid 函数。再次利用求导的链式法则，我们得到

$$\begin{aligned} \dfrac{\partial C_0}{\partial \omega^{(L)}} &= \sum\limits_{k=0}^{s_{L-1}-1}a_k^{(L-1)}g'\left(z^{(L)}\right)\left(a^{(L)} - y\right) \\ \\ \dfrac{\partial C_0}{\partial b^{(L)}} &= 1g'\left(z^{(L)}\right)\left(a^{(L)} - y\right) \\ \\ \dfrac{\partial C_0}{\partial a_k^{(L-1)}} &= \sum\limits_{j=0}^{s_L-1}\omega_{jk}^{(L)}g'\left(z^{(L)}\right)\left(a^{(L)} - y\right) \end{aligned}$$

于是我们得到了梯度矩阵 $\nabla C$，根据此我们便可以进行梯度下降。

具体过程

• 先进行一次前向传播

$$\begin{cases} z^{(l)} = \omega^{(l)}a^{(l-1)} + b^{(l)} \\ a^{(l)} = g\left(z^{(l)}\right) \end{cases}$$

• 计算输出层误差的方程，按定义有

  $$\delta_j^{(L)} = \dfrac{\partial C}{\partial z_j^{(L)}}$$

  由求导的链式法则得到

  $$\delta_j^{(L)} = \dfrac{\partial C}{\partial a_j^{(L)}} g'\left(z_j^{(L)}\right) \quad {(\text{BP}1)}$$

  写作矩阵形式为

  $$\delta^{(L)} = \nabla_aC \odot g'\left(z^{(L)}\right)$$

  若 $C$ 为均方误差，则

  $$\delta^{(L)} = (a^{(L)} - y) \odot g'\left(z^{(L)}\right)$$

  其中 $\odot$ 表示按元素的乘积，有时也被称为 Hadamard 乘积或 Schur 乘积。举例：

$$\begin{bmatrix}1 \\ 2\end{bmatrix} \odot \begin{bmatrix}3 \\ 4\end{bmatrix} = \begin{bmatrix}1 * 3 \\ 2 * 4\end{bmatrix} = \begin{bmatrix}3 \\ 8\end{bmatrix}$$

• 再通过下一层的误差 $\delta^{(l+1)}$ 表示当前层的误差 $\delta^{(l)}$

$$\delta^{(l)} = \left((\omega^{(l+1)})^\mathrm{T}\delta^{(l+1)}\right) \odot g'\left(z^{(l)}\right) \quad (\text{BP}2)$$

• 通过梯度下降更新权重 $\omega$ 和偏置值 $b$

$$\begin{cases} \omega_{jk}^{(l)} := \omega_{jk}^{(l)} - \dfrac{\partial C}{\partial \omega_{jk}^{(l)}} \\ \\ b_j^{(l)} := b_j^{(l)} - \dfrac{\partial C}{\partial b_j^{(l)}} \end{cases}$$

即

$$\begin{cases} \omega_{jk}^{(l)} := \omega_{jk}^{(l)} - a_k^{(l-1)}\delta_j^{(l)} \\ \\ b_j^{(l)} := b_j^{(l)} - \delta_j^{(l)} \end{cases}$$

下面给出 $(\text{BP}2)$ 的证明：

$$\begin{aligned} \delta^{(l)} &= \dfrac{\partial C}{\partial z^{(l)}} \\ \\ &= \dfrac{\partial C}{\partial z^{(l+1)}} \cdot \dfrac{\partial z^{(l+1)}}{\partial a^{(l)}} \cdot \dfrac{\partial a^{(l)}}{\partial z^{(l)}} \\ \\ &= (\delta^{(l+1)} \cdot \omega^{(l+1)}) \odot g'\left(z^{(l)}\right) \end{aligned}$$

由于 $\omega^{(l+1)}$ 维数为 $s_l \times s_{l+1}$，故上式也可以写作

$$\delta^{(l)} = ((\omega^{l+1})^\mathrm{T}\delta^{(l+1)}) \odot g'\left(z^{(l)}\right)$$

$(\text{BP}2)$ 得证。

Gradient checking

梯度检查是一个用来保证每次的前向传播、反向传播都是正确的算法。

当 $\theta \in \mathbb R$ 时，由于导数是图像上某一点处的斜率，我们通过取两点 $J(\theta + \epsilon)$ 和 $J(\theta - \epsilon)$，计算这两点连线的斜率 $l$，当 $\epsilon$ 很小时，$l$ 应当与导数相等，即

$$\dfrac{\mathrm d}{\mathrm d\theta} J(\theta) = \lim\limits_{\epsilon \to 0} \dfrac{J(\theta + \epsilon) - J(\theta - \epsilon)}{2\epsilon}$$

一般 $\epsilon$ 取 $10^{-4}$ 即可。

更普遍地，当 $\theta \in \mathbb{R}^n$ 时，此时 $\theta = \left[\theta_1, \theta_2, \dots, \theta_n\right]$，我们只需要对向量中每一个参数的偏导数都进行估计即可。具体地，

$$\dfrac{\partial}{\partial \theta_i}J(\theta) = \lim\limits_{\epsilon \to 0} \dfrac{J(\dots, \theta_{i - 1}, \theta_i + \epsilon, \theta_{i+1}, \dots) - J(\dots, \theta_{i - 1}, \theta_i - \epsilon, \theta_{i+1}, \dots)}{2\epsilon}$$

在 Matlab 中可以按如下方法进行计算：

for i = 1:n,
  thetaPlus = theta;
  thetaPlus(i) = thetaPlus(i) + EPSILON;
  thetaMinus = theta;
  thetaMinus(i) = thetaMinus(i) - EPSILON;
  gradApprox(i) = (J(thetaPlus) - J(thetaMinus)) / (2 * EPSILON);
end;
%Check that gradApprox = DVec%

在正式训练中不要使用梯度检查，因为计算代价相比于反向传播而言非常大。

Random initialization

在梯度下降时，对于参数 $\Theta$，我们需要给定其初值才能运行。
我们应当怎样对 $\Theta$ 设定初值呢？

一种可行的想法是，令

initialTheta = zeros(n, 1)

这在逻辑回归中是有效的，但这在神经网络中起不到任何作用。

这会表示所有神经元向下一层神经元的贡献全都为 $0$，下一层神经元的激活项全都相等，这会导致所有的 $\delta$ 值全都相等，所有的偏导数也全都相等。在每次梯度下降后， $\Theta$ 将会被更新为不为零但所有元素都相等的一个矩阵。

为了避免这种对称的情况，在神经网络中，对参数进行初始化时，我们需要使用随机初始化的思想。

具体地，令每个 $\Theta_{ij}^{(l)}$ 等于 $[-\epsilon, \epsilon]$ 内的一个随机数，即

$$-\epsilon \leq \Theta_{ij}^{(l)} \leq \epsilon$$

Matlab 举例：

Theta1 = rand(10, 11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(1, 11) * (2 * INIT_EPSILON) - INIT_EPSILON;

上面的 rand(x, y) 函数表示生成一个 $\text{x} \times \text{y}$ 的矩阵，其中的值都是 $[0, 1]$ 内的随机实数值。

Summarize

• 选择一个合适的神经网络架构：
  • 输入层单元个数为特征向量的维度；
  • 输出层单元个数为所要区分的类别个数。注意，每个数据的类别应当是一个向量，而不是一个实数。
  • 一般来说，默认只用一个隐藏层，如果使用多个隐藏层的话，默认每个隐藏层都具有相同数量的神经元。
• 训练神经网络：
  • 随机地初始化权重矩阵；
  • 对于每个训练数据 $x^{(i)}$，执行前向传播以得到输出 $h_\Theta(x^{(i)})$；
  • 计算代价函数 $J(\Theta)$；
  • 执行反向传播计算所有的偏导数 $\dfrac{\partial}{\partial \Theta_{jk}^{(l)}}J(\Theta)$；
  • 使用一次梯度检查来保证计算结果的正确性，然后禁用梯度检查；
  • 通过梯度下降或其他方法求出 $\underset{\Theta}{\arg\min}\ J(\Theta)$。